For 2D cellular automata (CA) there are 4-neighborhood and 9-neighborhood on a square grid. But it is much more natural to use a hexagonal grid (see Hexagonal Engineering for more information). I think for 3D CAs the "natural" structure is the the tetracaidecahedron. It is a 14-faced, space filling polyhedron. The following picture demonstrates the space filling attribute with some tetracaidecahedra:
(the source, with which I generated this picture with Povray)
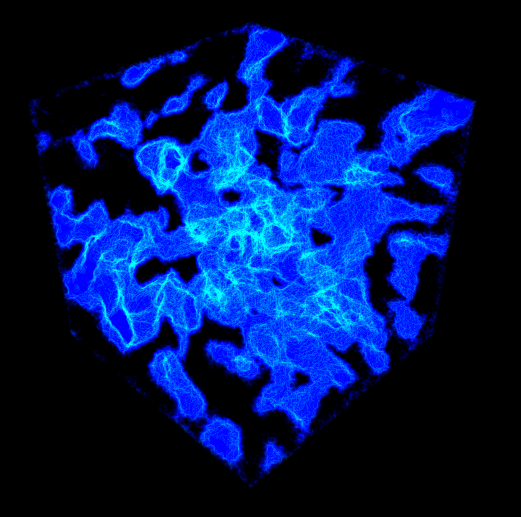
I've played a bit with a binary totalistic tetracaidecahedron cellular automaton and with rule B014S1237 (new cells are born on 0, 1 and 4 active neighbours and active cells survive on 1, 2, 3 and 7 active neighbours), the initial space filled with random active cells with a density of 30 %, a structure like the coral in my 2D Totalistic Explorer emerges after some time. A picture rendered from Povray with a DF3 file (128x128x128 voxels, produced from a Java program) for the interior of a box:
18. May 2003, Frank Buß