Polygonizer

Jules Bloomenthal wrote an article about an implicit surface polygonizer. I've ported his C program to Lisp. If you want to execute the polygonizer, you'll need lispbuilder-sdl, cl-opengl and optionally the Infix package for easier entering mathematical formulas.

How it works

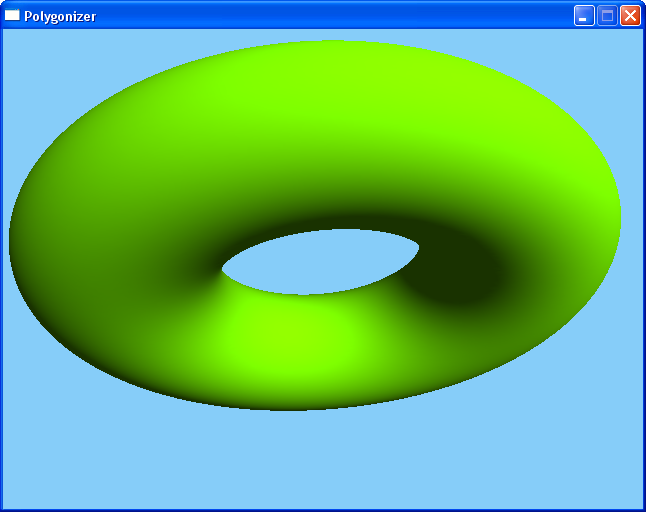
The polygonizer calculates the surface of a function. A point is on the surface of a function if the function value for this point is 0. A simple example is a torus:

(defun torus (x y z)
  "a torus"
  (let* ((major 2.5)
         (minor 1.2)
    (x2 (* x x))
         (y2 (* y y))
         (z2 (* z z))
         (a (+ x2 y2 z2 (* major major) (- (* minor minor)))))
    (- (* a a) (* 4.0 (* major major) (+ y2 z2)))))

Then we define a callback function, which is called by the polygonizer for every triangle it creates:

(defun triangle (p1 p2 p3 n1 n2 n3)
  (incf *triangle-count*)
  (gl:begin :triangles)
  (gl:normal (point-x n1) (point-y n1) (point-z n1))
  (gl:vertex (point-x p1) (point-y p1) (point-z p1))
  (gl:normal (point-x n2) (point-y n2) (point-z n2))
  (gl:vertex (point-x p2) (point-y p2) (point-z p2))
  (gl:normal (point-x n3) (point-y n3) (point-z n3))
  (gl:vertex (point-x p3) (point-y p3) (point-z p3))
  (gl:end))

After initializing OpenGL, we call the polygonizer:

(polygonize #'torus 0.10 100 0.0 0.0 0.0 #'triangle TET)

The output:

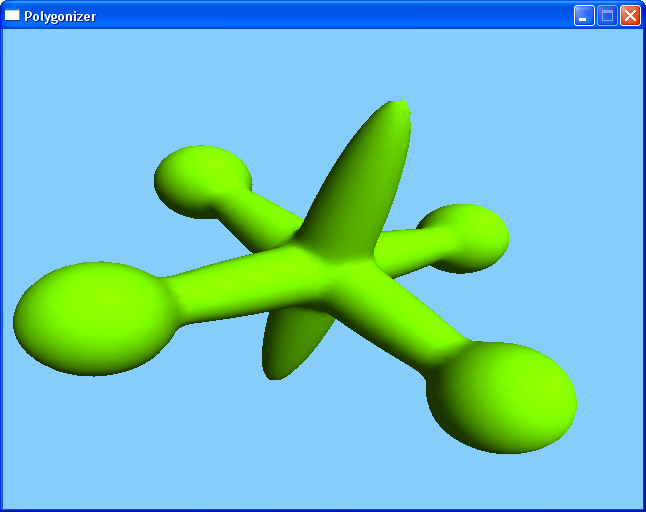
For more complex functions, like this one from the paper:

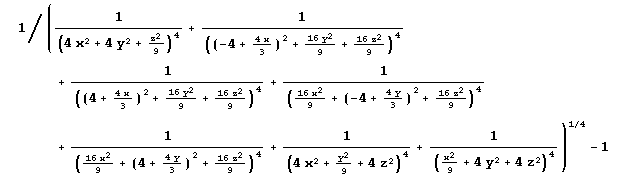
it is easier to use the Infix package, if you are not a hardcore Lisp programmer, to write it like this:

(defun jack (x y z)
  #I"(1/(x^^2/9+4*y^^2+4*z^^2)^^4
        +1/(y^^2/9+4*x^^2+4*z^^2)^^4
        +1/(z^^2/9+4*y^^2+4*x^^2)^^4
        +1/((4*x/3-4)^^2+16*y^^2/9+16*z^^2/9)^^4
        +1/((4*x/3+4)^^2+16*y^^2/9+16*z^^2/9)^^4
        +1/((4*y/3-4)^^2+16*x^^2/9+16*z^^2/9)^^4
        +1/((4*y/3+4)^^2+16*x^^2/9+16*z^^2/9)^^4)^^(-1/4)-1")

This produces the following surface:

The source in one file.