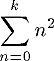
Meine bisherigen Versuche, eine generative Formel für eine Primzahl zu finden und die 250.000 Dollar beim EFF-Wettbewerb zu gewinnen, waren noch nicht erfolgreich. Es gibt zwar einen interessanten Algorithmus, der aber zu langsam ist. Vielleicht liegt das auch daran, daß die Primzahlen so elementar sind, daß man gar keine Formel dafür finden kann. Zumindest hat es den Anschein, als würde da viel Information drin stecken. Wenn man z.B. die Elemente der Folge
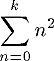
dafür verwendet, in einem Bild die Punkte einzufärben, dann kommt dabei ein schräger Strich heraus, wenn man folgenden einfachen Turtle-Algorithmus verwendet:
for ("p" in "Folge") {
m := p modulo 11
if m = 1 then "gehe eins nach oben"
if m = 2 then "gehe eins nach unten"
if m = 3 then "gehe eins nach links"
if m = 4 then "gehe eins nach rechts"
"erhöhe abschließend den Farbwert an der aktuellen Stelle"
}
Führt man den Algorithmus dagegen mit der Primzahlfolge aus, dann kann man
damit folgendes Bild erzeugen:

Das Verfahren habe ich auf der Web-Seite http://yoyo.cc.monash.edu.au/~bunyip/primes/index.html entdeckt, auf der allerdings der Algorithmus fehlerhaft beschrieben wird (die Zeile "else if(x=5) move position up" in der Originalbeschreibung war zuviel). Im folgenden Applet ist er richtig implementiert. Zum Vergleich kann man auch andere Folgen als die Primzahlen anzeigen. "Obere Grenze" gibt die größte zu berechnende Primzahl bei Primzahlen an, oder die Anzahl Elemente bei den anderen Formeln. Bei der Primzahlfolge wird es ab 10 Millionen als obere Grenze interessant, wenn der Computer schnell genug ist :-)
Der Quelltext besteht aus zwei Klassen: Fraktal.java und FraktalCanvas.java. Er ist so strukturiert, daß leicht neue Formeln oder andere Darstellungsarten eingebaut werden können.
Ein anderer Ansatz, Primzahlen darzustellen, könnte mit Hilfe der Zeta-Funktion funktionieren:
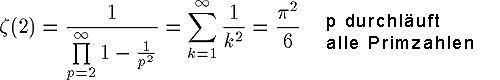
Wenn es gelingen würde, das irgendwie geometrisch zu deuten, dann entsteht dabei bestimmt eine interessante Grafik.