 (as PDF)
(as Postscript)
(as PDF)
(as Postscript)This challenge is over, see Marsrescue for a new challenge.
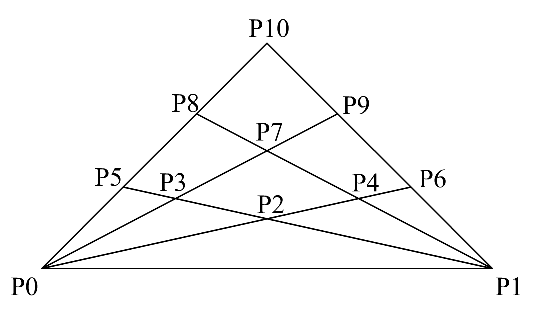
The challenge is to write a program, which counts all triangles with area >0 in this figure: (all figures are available in PDF and Postscript, too, for printing, if someone wants to use it as a homework assignment or something like this)
 (as PDF)
(as Postscript)
(as PDF)
(as Postscript)
But count only the triangles, which are bounded by lines, like (P0, P7, P8), not all possible connections between the points, like (P7, P8, P9). If anything is unclear, the solution is 27 and looks like this:
 (as PDF)
(as Postscript)
(as PDF)
(as Postscript)
All programs should be documented enough to understand how it works and it should not simply print 27, but somewhere it should read from a file or integrate the points and geometry, so that it is easy to change it for similar problems, for example if another line is added, but it need not to be so general to count the number of squares. An example:
 (as PDF)
(as Postscript)
(as PDF)
(as Postscript)
Graphic output is not needed, but you can do what you want. If a GUI or something else is included, would be nice to write each times: how long you needed for the pure algorithm and for the rest.
This is not a quantitative, but more a qualitative challenge. Not the number of lines or the time (which I can't verify anyway) is important, but I'm interested in good solutions, which shows the advantages of the choosen language.
The challenge is over and there are some nice solutions. In general it shows that the language doesn't matter that much, but the idea is more important. The ultimate short solution is a mathematical formula, which is faster and shorter than every other solution, which counts all triangles by program. Comparing the other solutions shows, that you have to choose the right idea for your language. The solution in Haskell can be expressed very compact with list comprehension, but the same idea is more difficult to express in other languages.
| Language | Author and Solution |
Solution Characterizing (needs to be completed, any volunteer?) | Lines of Code | Time | Comment |
|---|---|---|---|---|---|
| Lisp |
|
Geometric, input is the coordinates of the points, and a list of set of aligned points, outputs a list of tri-points. Additional GUI draw the triangles. | all: 183 algorithm only, without GUI and without comments: 84
|
3 hours: - 20 min: painting graphics and sampling the point-coordinates and geometry |
I'm a Lisp newbie and I think the program size and time to implement could be halfed, if a Lisp master implements it, but with the help of the interactive REPL it was not too difficult for me. The GUI with the CLIM library took so long, because this is my first program which uses this library. |
| Lisp |
|
Symbolic, input is a list of set of aligned points, prints list of tri-points and returns count. Prints the count and triangles for all sets of aligned points (two segments on a line would specify 12 segments). | 37
|
26 minutes |
|
| Ruby |
|
75 | ? | ||
| Lisp |
|
Symbolic, input is a list of adjacent aligned segments. Output is the list of tri-points. (two segments on a line specify only two segments). | with comments: 42 | ~30 minutes (~40 with documentation after) |
Comment from the author: To show off some of Lisp's strength, I tried to define the triangle in terms of lists and segments, with points being able to call ASSOC to get a list of all points the connect to any other given point. I used a global (dynamic) variable to hold the solution to the problem, because it was easier to do, ATM. |
| Lisp | Tayssir John Gabbour
|
37 lines without blank lines | 30min +/- 5min for answer 10min to remove unused code, tediously eyeball whether it actually gave correct triangles, and write these comments |
||
| Lisp |
|
40 | It took about 20 minutes to write, and another 10 minutes to see why I was getting only 23 triangles (I had a line consisting of P0, P4, p8, p10) rather than 27. | Comment from the author: I do not consider myself a lisp expert, and it clearly is using too much free store. Style suggests I should use better names, less global values etc. I should probably figure out how to return early from 'line2' and 'line3'. |
|
| Lisp | 15 | 17 minutes for the solution here, plus about 8 minutes on a different initial solution before I realised it couldn't work | |||
| Lisp | 80 | 1 hour 15 mintues | |||
| C++ | 60 | 1 hour | Comment from the author: The solution below uses the free software computer algebra C++ library GiNaC to solve the problem. The output of the program is also shown below. The library can be obtained at http://www.ginac.de/. Comment from Frank: With GiNaC you can do Lisp-like-looking programms in C++, for example: symbol x("x"),y("y"); |
||
| C++ |
|
207 (136 without comments and empty lines) | about 2 hours (1 to write + 1 to test and bugfixing) | ||
| Scheme |
PLT-Scheme solution, which returns the triangles
|
Mathematical, input is the number of additional points on the left and right side of an enclosing triangle, output is the number of sub- triangle. The program implements the mathematic formula computing the count. Comment from Frank: Konstantin's formula shows that it could be done easier, and of course, Mathematica says that Binomial(n+1,2)*(m+1)+Binomial(m+1,2)*(n+1)+(n+1)*(m+1) is the same as (1/2)*(1+m)*(1+n)*(2+m+n). |
66, nice documented with ASCII graphics comments 12 without comments and empty lines |
80 min: - 45 min thinking and drawing triangles |
Comment from Frank: This is a very different solution, because he found a formula for calculating the number of triangles which results in criss-crossing inside a triangle. |
| Lisp |
|
25 non-blank lines | 14 minutes | ||
| Java |
|
51 (28 without comments and empty lines) | ? | ||
| Lisp |
|
67 | 75 minutes: - 30 minutes coding the solution |
Comment from the author: I'm still getting familiar with Lisp (and macros in particular) | |
| C++ |
|
79 (49 without comments and empty lines) | 92 minutes: - 17 to write
|
Comment from the author: This solution favours simplicity over performance. | |
| Lisp | Alan S. Crowe | - 67 first version - 60 second version |
- 25 minutes to write the first working version. - 25 more minutes generates two more versions of the code, neither much of an improvement. |
||
| Haskell | Dirk Thierbach (generalized for polygons) | 93, written in Literate Haskell mode, the pure algorithm is only 6 lines long | ca. half an hour for the first version | Comment from Frank: This shows the elegance of pure functional languages. Perhaps it could be done in Lisp the same, but it wouldn't look so nice without list comprehensions. Very detailed comments in Literate Haskell (the comments are normal text and the program is indented). Comment from the author: I didn't measure the exact time I needed to program it, because I was interrupted frequently, anyway, but I needed maybe half an hour for the simple version (most of it writing auxiliary functions that turned out to be unnecessary), and maybe another half an hour for the two refined versions and the literate comments. |
|
| Kogut | Marcin 'Qrczak' Kowalczyk | 29 | 30 minutes: - First buggy version - 13 minutes - Bug fixing (adding missing line [0 1], and correcting the logic to not try to constrain the ordering of lines because the ordering of points already ensures that each solution is counted once) - 20 minutes since beginning - Formatting, comments, using better names which made comments redundant, removing redundant comments - 30 minutes since beginning |
||
| Java | Filip Larsen | 84 | ca. 90 minutes | ||
| Python | Marco Wahl | 94 (15 without comments and empty lines) | ? Started the challenge sunday 4 p.m. --- had some good time with it --- and stopped 10 p.m. |
||
| Lisp | Björn Lindberg |
|
13 (10 lines for the only one main function) + 26 lines of documentation | It took almost an hour to code, but almost half of that was spent on tracking down a thinko in using LOOP. | |
| Java | Babu Kalakrishnan | 181 | 40 minutes: Coding : 25 minutes |
||
| Lisp | Gabor Melis | 47 (without comments and empty lines: 34) | |||
| Lisp | Ørnulf Staff | first solution: 22 second solution: 17 |
Work time for this was approx. 1 hour including 15 minutes spent on a non-starter first attempt. | ||
| Lisp | Espen Wiborg | 60 | 45 minutes (Wallclock time spent: 2 hours) |
||
| Lisp | Mark McConnell | 126 lines. That includes 16 blank lines and 10 lines of documentation, making (by chance) exactly 100 lines of code. | 1 hr 22 min | Comment from the author:
You can enter any number of lines. We assume any point of intersection of two lines is part of the puzzle. You *don't* have to enter all the points, just enough to specify all the lines (in the test example, P0, P5, P8, P10, P9, P6, P1). We also assume all lines and points are rational (integer or integer/integer), not floating-point. Cool Lispy features: built-in rational arithmetic, remove-duplicates, count-if. This solution is not optimized for zillions of points, since the challenge was to write something fast. Optimization 1: get rid of remove-duplicates. Redefine pt and line with defstruct so that equalp works by checking their slots. In each line, divide through by the leftmost non-zero coefficient so the first non-zero entry becomes 1; this makes equalp detect when two lines are equal. Then use an equalp hash-table to remove duplicates. Optimization 2 [more important]: don't enumerate all triples of points. Make a table that, for each point p, gives all points q connected to p by a line of the diagram. Do some kind of double-search on this table to find triangles. Use lexicographic sorting on the points to find each triangle once, not 3! = 6 times. |
|
| Lisp | Sergey Kataev | 20 (without comments and empty lines: 11) | 90 minutes, with some distractions, hyperspec research and making source look nice. | ||
| Java | Larry Coon | 46 (without comments and empty lines: 30) | 19 minutes (14 for first draft, 5 extra to fix "colinear" problem) | ||
| C++ | Bunny | 162 (without comments and empty lines: 104) | about 45 mins |
comment from the author: far too much of the time spent was farting round with the STL | |
| J | Konstantin L. Metlov | Mathematical, input is the number of additional points +1 on the left and right side of an enclosing triangle, output is the number of sub- triangle. The program implements the mathematic formula computing the count. | 1 (first version: 3 characters, second version: 6 characters) | it took me 15-20 minutes of drawing rectangles to derive the formula. |
comment from Frank: This is a nice solution and the language looks interesting. It is the same concept as the Scheme solution, which uses a formula instead of counting the triangles, but this formula is much easier than the one used in the Scheme solution. |
| Lisp | Brian Caruso | 128 lines of text, aprox. 60 lines of comments | 2.5 hours | ||
| Lisp | Vasilis Margioulas | 57 | ~ 1 hour | ||
| AWK | Ed | 59 | ~ 1 hr 45 min | ||
| Lisp | Lawrence Kesteloot | 43 | 30 minutes | comment from the author: I started learning Lisp last week. Much of the time here was spent trying to figure out which keywords of "loop" I needed. | |
| I received the following solutions after the end of the challenge, so it may be derived from the other solutions, because I published all previous solutions after the end. | |||||
| JavaScript | Wolfgang Zeidler (HTML with JavaScript, text-only) | 35 (without comments and empty lines: 26) | 20 minutes | comment from Frank: was sent just after I posted the end of the challenge and the solutions, but I don't think that it is derived from any other solution. | |
| Matlab | Urs | 9 lines of relevant code (not yet optimized) |
5 minutes | ||
| D | Stewart Gordon |
185 minutes: Theory: determining the number 30 |
comment from Frank: very detailed documentation as an external file with matematical explanations and nice GUI program, which shows all triangles. | ||
| Python | Todd DeLuca | 16 (13 without comments and whitespaces) | ~3 hours | comment from the author: reimplementation of Paul Foley's Lisp solution in Python | |
| C | Paul Hsieh | 93 (30 lines for the core algorithm) | 17 minutes | ||
| SQL | Adam Musch |
60 | ? | ||
| SETL2: ftp://anonymouse@cs.nyu.edu/pub/languages/setl2/, http://www.settheory.com/ |
Georg Bauhaus | 96 | ? | ||
| Prolog | Sean, posted on Slashdot | 35 lines of code |
about 45min (mostly remembering syntax & predicates) | comment from the author: it's definately simpler than any of the other solutions. | |
| C | Derek | 38 | ~30 minutes | comment from the author: I looked at the previous entries to get an idea of the algorithm, then I implemented it in C with a focus on using ASCII strings to describe the line segments, and 'chars' to describe the points P0 to P10. The only oddity with this approach is that P10 is indicated by the character ':'. | |
| OCaml | Andrew Kensler |
comment from the author: My solutions were based on the observation that
the "triangle" is a distortion of a rectangle. All valid sub-triangles
map to sub-rectangles bordering along at least one of two adjacent edges.
Each of the functions that I wrote takes a pair of numbers, giving the number
of divisions along each edge.
I first did it using through brute force using the imperative features in OCaml (roughly 5-10 minutes, 13 lines minus blank lines and comments). Then, I converted that to a purely-functional, tail-recursive style (roughly 15-20 minutes and 10 lines). Lastly I realized that the symmetry made a formula possible, which I derived and coded (roughly another 20 minutes and 4 lines). |
|||
| Mathematica | Larry Morris |
6 | 14 minutes | It took about 14 minutes for me to write these 6 lines of Mathematica code for counting triangles. This solution works by listing all possible triads of points p0..p10 and then selecting the ones from that list that have exactly two points in common with each of exactly three separate lines. No reference was made to any of the previous solutions, except to note that the Matlab solution was done in 5 minutes. |
|
| Ch | Xiaodong Zhou | The total number of code lines is 27, and 35 with comments. | Time to make it work in Ch takes 30 seconds for the change. | This version of Ch code is modified based on Derek's original C code with fewer lines. |
|
| Mathematica | Justin DSC Kaeser |
6 | a few hours | Programming language is Mathematica, and it took me a few hours to do, mostly figuring out details of Mathematica pattern matching. Like the other Mathematica solution it's 6 lines long and general enough to find triangles in any construction of lines with given intersection points. However mine is noticeably slower - but I mainly did it to see what I could do with the pattern matching capabilities of Mathematica. | |
| Perl | Gim Hong Tan | 42 | |||
JAS in PJB = FB = MB = IS = PF = JN in JM
JAS /= PJB JN /= JM